Jon's Big Theory

The universe is an anti de-sitter space within an all but equal and opposite de sitter space.

The zero point energy density of the vacuum is masked by the zero point curvature of space-time.

The fourth dimension squared equals cosmological time squared minus one.

Everything in the universe is made from Left Over Vacuum Energy.

_______________________________________________________________________________________________

Time and The Fourth Dimension.

Stephen Hawking and Leonard Mlodinow state in The Grand Design (page 172)

In the early universe -- when the universe was small enough to be governed by both general relativity and quantum theory -- there were effectively four dimensions of space and none of time.

...

Suppose the beginning of the universe was like the South Pole of the earth, with degrees of latitude playing the role of time. As one moves north, the circles of constant latitude, representing the size of the universe, would expand. The universe would start as a point at the South Pole, but the South Pole is much like any other point. To ask what happened before the beginning of the universe would become a meaningless question, because there is nothing south of the South Pole. In this picture space-time has no boundary -- the same laws of nature hold at the South Pole as in other places.

_______________________________________________________________________________________________

The Fourth Dimension Squared Equals Cosmological Time Squared Minus One.

How would it be possible for the fourth dimension to be a dimension of space in the early universe and be the dimension of time that we all know and love today? Let's start with pure time, and then add a single unit of space.

When time and space are added together the square of the result is the difference of the squares of the parts. If there is more time than space then the result is time. It there is more space than time then the result is space. If the two are equal then the result is null.

So if we use u as the co-ordinate of the fourth dimension and t as a measure of cosmological time then

${\displaystyle u^{2}=t^{2}-1}$

For t between zero and one the fourth dimension would be a dimension of space, for t greater than one the fourth dimension would be a dimension of time, and for t much greater than one the fourth dimension would be an almost uniform dimension of time.

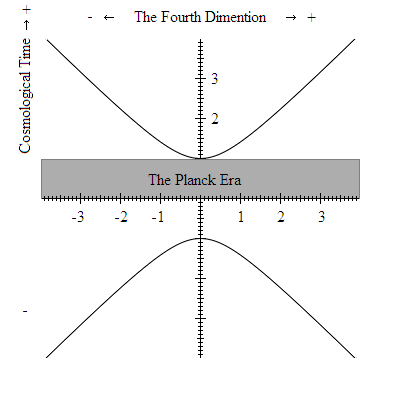
The period when cosmological time had values between zero and one is known as The Planck Era. It could be said that during the Planck Era the fourth dimension was a dimension of space. However, if we look at the graph we see a different story.

There are positive and negative values of u and there are positive and negative values of t, but while we can move from negative u to positive u there is no route from negative t to positive t. Time has a beginning, even though the fourth dimension does not.

Furthermore, time does not begin at zero, time begins when the fourth dimension is zero. Time begins at one. Therefore there was no Planck Era.

_______________________________________________________________________________________________

Derivatives of u and t 

${\displaystyle from\ \ \ u^{2}=t^{2}-1\ \ \ it\ follows\ that}$

${\displaystyle u=\pm \left(t^{2}-1\right)^{1/2}}$

${\displaystyle {\frac {du}{dt}}=\pm {\tfrac {1}{2}}\left(t^{2}-1\right)^{-1/2}\left(2t\right)=\pm {\frac {t}{u}}}$

${\displaystyle \left({\frac {du}{dt}}\right)^{2}={\frac {t^{2}}{u^{2}}}}$

${\displaystyle \left({\frac {dt}{du}}\right)^{2}={\frac {u^{2}}{t^{2}}}}$

_______________________________________________________________________________________________

Change Of Co-ordinates

${\displaystyle {\text{The general formula for a change of co-ordinate of a tensor }}F_{t}{\text{ is }}}$

${\displaystyle F_{t}=F_{r}{\dfrac {\partial r}{\partial t}}+F_{\theta }{\dfrac {\partial \theta }{\partial t}}+F_{\phi }{\dfrac {\partial \phi }{\partial t}}+F_{u}{\dfrac {\partial u}{\partial t}}}$

${\displaystyle {\text{since }}t{\text{ is only dependant on }}u{\text{, and is fully dependant on }}u{\text{, this simplifies to}}}$

${\displaystyle F_{t}=F_{u}{\dfrac {du}{dt}}}$

${\displaystyle {\text{likewise for }}F_{tt}}$

${\displaystyle F_{tt}=F_{uu}\left({\dfrac {du}{dt}}\right)^{2}}$

_______________________________________________________________________________________________

The cosmological constant and zero point values

Einstein's field equations may be written

${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }=\kappa T_{\mu \nu }}$

alternatively, using zero point values we get

${\displaystyle G_{\mu \nu }+G_{\mu \nu }^{^{_{ZP}}}=\kappa T_{\mu \nu }+\kappa T_{\mu \nu }^{^{_{ZP}}}}$

${\displaystyle {\text{Where }}G_{\mu \nu }^{^{_{ZP}}}{\text{is the zero point curvature of space time }}}$

${\displaystyle {\text{and }}T_{\mu \nu }^{^{_{ZP}}}{\text{is the zero point stress energy of the vacuum.}}}$

Subtracting the second equation from the first

${\displaystyle \Lambda g_{\mu \nu }-G_{\mu \nu }^{^{_{ZP}}}=-\kappa T_{\mu \nu }^{^{_{ZP}}}}$

${\displaystyle \Lambda ={\frac {G_{\mu \nu }^{^{_{ZP}}}}{g_{\mu \nu }}}-{\frac {\kappa T_{\mu \nu }^{^{_{ZP}}}}{g_{\mu \nu }}}}$

If the cosmological constant is the difference of two zero point values then we can have the Casimir Effect without the Vacuum Catastrophe, although a non-zero value would still be subject to the fine tuning problem.

If the fourth dimension were a uniform dimension of time then this might be all that there was to say on the matter. However, if it is not, then we may make the further assumption that the curvature tensor is subject to the fourth dimension and the stress-energy tensor is subject to proper time. Thus allowing us to modify Einstein's Field Equations.

_______________________________________________________________________________________________

Modifying Einstein's Field Equations

The six spacial equations remain unchanged and can be written either way

${\displaystyle G_{ij}+\Lambda g_{ij}=\kappa T_{ij}}$

${\displaystyle G_{ij}+G_{ij}^{^{_{ZP}}}=\kappa T_{ij}+\kappa T_{ij}^{^{_{ZP}}}}$

The three mixed equations become

${\displaystyle G_{iu}+G_{iu}^{^{_{ZP}}}=\kappa T_{it}+\kappa T_{it}^{^{_{ZP}}}}$

and the temporal equation becomes

${\displaystyle G_{uu}+G_{uu}^{^{_{ZP}}}=\kappa T_{tt}+\kappa T_{tt}^{^{_{ZP}}}}$

Taking this last equation and incorporating the cosmological constant

${\displaystyle \Lambda g_{uu}-G_{uu}^{^{_{ZP}}}=-\kappa T_{uu}^{^{_{ZP}}}}$

we get

${\displaystyle \Lambda g_{uu}-G_{uu}^{^{_{ZP}}}+G_{uu}+G_{uu}^{^{_{ZP}}}=\kappa T_{tt}+\kappa T_{tt}^{^{_{ZP}}}-\kappa T_{uu}^{^{_{ZP}}}}$

${\displaystyle G_{uu}+\Lambda g_{uu}=\kappa T_{tt}+\kappa T_{tt}^{^{_{ZP}}}-\kappa T_{uu}^{^{_{ZP}}}}$

${\displaystyle G_{uu}+\Lambda g_{uu}=\kappa T_{tt}+\kappa T_{tt}^{^{_{ZP}}}-\kappa T_{uu}^{^{_{ZP}}}\left({\frac {du}{dt}}\right)^{2}\left({\frac {dt}{du}}\right)^{2}}$

${\displaystyle G_{uu}+\Lambda g_{uu}=\kappa T_{tt}+\kappa T_{tt}^{^{_{ZP}}}-\kappa T_{tt}^{^{_{ZP}}}{\frac {u^{2}}{t^{2}}}}$

${\displaystyle G_{uu}+\Lambda g_{uu}=\kappa T_{tt}+\kappa T_{tt}^{^{_{ZP}}}\left(1-{\frac {u^{2}}{t^{2}}}\right)}$

${\displaystyle G_{uu}+\Lambda g_{uu}=\kappa T_{tt}+{\frac {\kappa }{t^{2}}}T_{tt}^{^{_{ZP}}}}$

${\displaystyle {\frac {1}{t^{2}}}T_{tt}^{^{_{ZP}}}{\text{ is the Left Over Vacuum Energy.}}}$

_______________________________________________________________________________________________

Re-deriving The Friedman Equation

${\displaystyle {\text{ }}}$

${\displaystyle {\text{The general FLRW metric, using spherical coordinates, can be re-written. }}}$

${\displaystyle \mathrm {d} s^{2}=-c^{2}\mathrm {d} u^{2}+{a}^{2}\left({\frac {\mathrm {d} r^{2}}{1-kr^{2}}}+r^{2}\mathrm {d} \theta ^{2}+r^{2}\sin ^{2}\theta \,\mathrm {d} \phi ^{2}\right)}$

${\displaystyle {\text{Where:}}}$

${\displaystyle r,\theta (theta),\phi (phi){\text{ are the normal polar co-ordinates of space.}}}$

${\displaystyle u{\text{ is the co-ordinate of the fourth dimension.}}}$

${\displaystyle a{\text{ is the scale factor and is taken to be a function of time.}}}$

${\displaystyle k{\text{ is the curvature index, and is taken to belong to the set (-1,0,+1).}}}$

${\displaystyle {\text{ }}}$

${\displaystyle {\text{Solving the first of Einstein's field equations we get }}}$

${\displaystyle G_{uu}=3{\frac {\left(da/du\right)^{2}+kc^{2}}{a^{2}}}}$

${\displaystyle G_{uu}+\Lambda g_{uu}=\kappa T_{tt}+{\frac {\kappa }{t^{2}}}T_{tt}^{^{_{ZP}}}}$

${\displaystyle 3{\frac {(da/du)^{2}}{a^{2}}}=\kappa T_{tt}+{\frac {\kappa }{t^{2}}}T_{tt}^{^{_{ZP}}}+\Lambda c^{2}-3{\frac {kc^{2}}{a^{2}}}}$

${\displaystyle {\text{ }}}$

${\displaystyle {\text{It is known from present observations that the value of the Cosmological Constant is extremely }}}$ ${\displaystyle {\text{small if not zero and can therefore be ignored in the early universe. }}}$ ${\displaystyle {\text{If we assume that the universe started as a vacuum then the only terms left of significance are }}}$ ${\displaystyle {\text{Left Over Vacuum Energy and Intrinsic Curvature. It therefore follows that }}}$

${\displaystyle {\text{ }}}$

${\displaystyle 3{\frac {(da/du)^{2}}{a^{2}}}={\frac {\kappa }{t^{2}}}T_{tt}^{^{_{ZP}}}-3{\frac {kc^{2}}{a^{2}}}}$

Assuming that in fundamental units the zero point energy density of the vacuum has a value of 1, i.e. enough to cause the full on Vacuum Catastrophe if it were not for the zero point curvature of space-time; and then solving for the simplest case where the intrinsic curvature is zero.

${\displaystyle 3{\frac {(da/du)^{2}}{a^{2}}}={\frac {\kappa }{t^{2}}}}$

${\displaystyle {\frac {(da/du)^{2}}{a^{2}}}={\frac {\kappa }{3}}{\frac {1}{t^{2}}}}$

${\displaystyle {\frac {da/du}{a}}={\sqrt {\frac {\kappa }{3}}}{\frac {1}{t}}}$

${\displaystyle \int {\frac {da/du}{a}}du={\sqrt {\frac {\kappa }{3}}}\int {\frac {1}{t}}du}$

${\displaystyle ln\left(a\right)={\sqrt {\frac {\kappa }{3}}}\ ln\left(t+u\right)\ +\ constant\ of\ integration}$

${\displaystyle a\propto \left(t+u\right)^{\sqrt {\kappa /3}}}$

${\displaystyle a\propto \left(t+{\sqrt {t^{2}-1}}\right)^{\sqrt {\kappa /3}}}$

${\displaystyle {\text{So there we have it. Inflation, slow roll, with a graceful exit, straight from the vacuum; }}}$ ${\displaystyle {\text{providing that κ in natural units is more than three. At the beginning of time the scale }}}$ ${\displaystyle {\text{factor was proportional to one, so in this model the universe began with a non-zero }}}$ ${\displaystyle {\text{spacial size, there was no singularity.}}}$

_______________________________________________________________________________________________